1. What you need before starting.

2. This example analysis.

In this example script our aim is to demonstrate how reliability analyses can be conducted in R and thus we present only some of the analytical tools available. We do not attempt to provide an exhaustive coverage of the topic and recommend that those wishing to undertake such analyses consult the relevant texts and literature beforehand. The Meeker and Escobar (1998) text (see “References cited” below) provides a comprehensive coverage.

1. Load required packages, functions and datasets.

Firstly, we need to load the SPREDA, boot, and lattice packages:

library(SPREDA)
library(boot)
library(lattice)

For a brief overview of R packages you can type commands such as library(help="SPREDA") or help("SPREDA-package"). Next, load the file ReliabilitySupportFns.R, which contains additional functions that we’ll be using.

source("https://raw.githubusercontent.com/CodeOwl94/ross-reliability/master/ReliabilitySupportFns.R")

Next we need to load the dataset. Here, we load a comma separated values (csv) file:

exa1 <- read.csv("https://raw.githubusercontent.com/CodeOwl94/ross-reliability/master/EXA1.csv",
                 header=T)
dim(exa1)

## [1] 127   2

A csv file can be prepared by saving these data, once appropriately formatted (see below) in an MS Excel worksheet, as this type of file using the “Save As” option, as selected from the “File” menu in Excel. The header=T argument is specified as we wish to retain the appropriately labelled data columns within the data frame object, which R converts it into, by default.

NOTE: If, after stepping through this example script, you wish to apply these functions to analyse your own dataset, you will need to firstly reformat your data into a .csv file, and then load it into R, as demonstrated above. However you will need to enter your file name as the first argument of the read.csv() function instead. There are other ways of importing data into R, but if you need more information about this method, type the command help(read.csv).

Our data appear to have been read into R OK; we know this because the dim() function returned the values 127 and 2, which correspond to the 127 rows and 2 columns of data in the original data file. Always check this, as errors may occur in this step, such as columns of missing values or due to extra commas in the dataset prior to csv file conversion. Now, lets have a look at these data:

head(exa1) # returns the first 6 rows:

##   fail time
## 1    F   57
## 2    F    7
## 3    F   21
## 4    F    7
## 5    S   76
## 6    F   22

stack(table(exa1$fail))

##   values ind
## 1    123   F
## 2      4   S

Prior to importing this file, we coded the values in the fail column as:

• F, Failure: a valid time-to-failure measurement, or
• S, Suspension: a right censored measurement.

It is sensible to code observations in a manner that helps us to clearly identify what they represent. However, now we need to recode these fail values into values of 1 and 0 respectively, because the SPREDA package recognises this binary coding for fail data:

• 1, Failure: a valid time-to-failure measurement, or
• 0, Suspension: a right censored measurement.

exa1$fail <- ifelse(exa1$fail=="S","T",as.character(exa1$fail))
exa1.dat <- data.frame(time=exa1$time,
                       event=1-as.numeric(as.logical(exa1$fail)))
stack(table(exa1.dat$event))                       

##   values ind
## 1      4   0
## 2    123   1

The ifelse() function is necessary to code the suspensions so that the subsequent line can format fail appropriately. If the data were complete time-to-failure measurements (i.e., no censored data) the ifelse() statement can be omitted.

str(exa1.dat)

## 'data.frame':    127 obs. of  2 variables:
##  $ time : int  57 7 21 7 76 22 51 27 8 18 ...
##  $ event: num  1 1 1 1 0 1 1 1 1 1 ...

head(exa1.dat)

##   time event
## 1   57     1
## 2    7     1
## 3   21     1
## 4    7     1
## 5   76     0
## 6   22     1

The fifth row contains a censored measurement.

2. Graphical analysis.

Now lets look at these data. Importantly, this step helps to understand these data prior to fitting any models or making strong model assumptions (Meeker and Escobar, 1998). Results will inform initial decisions made during subsequent model fitting.

Plot.Observations(exa1.dat)
title("Figure 1", adj=1)

This figure shows the sorted raw failure times, with censored times coloured in red. This is a little difficult to see, so instead we plot for subsets of these data. First, we look at the observations ranked 1 to 60, in terms of time measurement (low to high):

Plot.Observations(exa1.dat[order(exa1.dat$time),][1:60,])
title("Figure 2", adj=1)

The 47.5th ranked observation, which is tied with three other measurements, is a right-censored measurement or suspension. Zooming in on the remaining time measurements (longer operating times):

Plot.Observations(exa1.dat[order(exa1.dat$time),][61:nrow(exa1.dat),],
                  Ntotal=nrow(exa1.dat))
title("Figure 3", adj=1)

The second argument in Plot.Observations() is required if the subset does not start at observation 1. We see that three other censored measurements occur at ranks 74, 103.5, 124. These rankings of censored observations, in order of total running time, were obtained using

sort(rank(exa1.dat$time,ties.method="average")[exa1.dat$event==0])

## [1]  47.5  74.0 103.5 124.0

OK. Now, let’s have a look at the empirical cumulative frequency distribution of the complete time-to-failure measurements.

plot(ecdf(exa1.dat[exa1.dat$event==1,"time"]),main="",xlab="time",
     verticals=T,las=1,adj=0.5) 
abline(v=quantile(exa1.dat[exa1.dat$event==1,"time"],probs=c(0.25,0.5,0.75)),
                  col='red',lwd=2,lty=2) # add on quartiles
title("Figure 4", adj=1)

Later, we adjust these relative frequencies for the censored observations to obtain non-parametric estimates of the probability of failure with time, \(F(t)\).

Next we can inspect the sampled frequencies as a histogram:

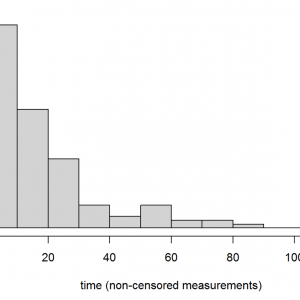
hist(exa1.dat[exa1.dat$event==1,"time"],main="",col="lightgrey",
     xlab="time (non-censored measurements)",las=1,adj=0.5)
title("Figure 5", adj=1)

Right-skewed distributions are typical of reliability data. Are these data from a single distribution? If there are unusual (e.g. multi-modal) patterns it might be worth seeking additional information about how these data were sampled. Also, we can return the plotted values by assigning the above command to a named object (exa1.hist), setting the plot=F argument, and inspecting the named elements of the returned list object.

exa1.hist <- hist(exa1.dat$time,plot=F)
attach(exa1.hist) # makes the list element names of exa1.hist into global objects.
data.frame(time=mids,n=counts)

##    time  n
## 1     5 54
## 2    15 32
## 3    25 19
## 4    35  6
## 5    45  3
## 6    55  6
## 7    65  2
## 8    75  3
## 9    85  1
## 10   95  0
## 11  105  0
## 12  115  1

detach(exa1.hist) # removes attached exa1.hist elements from the workspace.
rm(exa1.hist) # removes exa1.hist from our workspace, as we are finished with it.

The printed data frame shows the sampled frequencies of failure time measurements (n, column 2) alongside the mid-points of time for each time bin in the histogram, which gives us a better feel for these data. This table shows that the majority of failures (i.e., approximately 85 % of non-censored measurements) occurred prior to time 30, with small sample sizes for bins thereafter (and especially after time 60), which should be borne in mind when interpretting results.

Next we construct probability plots, as suggested in Meeker and Escobar (1998), to identify which distribution(s) may provide a good approximation of these data.

Probability.Plots(exa1.dat)

## [1] "Adjustments to 95 % simultaneous confidence bounds to account for"
## [1] "non-increasing values follow method of Meeker & Escobar (1998)"

# title("Figure 6", adj=1)

These plots can be interpretted thus:

• If the points lie in a straight line then this suggests that the corresponding distribution may be suitable for modelling this dataset.
• 95 % simultaneous confidence bands show the uncertainty for these measurements across the range of sampled times
• If a linear fit to these data falls within these bounds (i.e., from the next step of this analysis) that is further evidence in support of that distribution.

Probability.Plots(exa1.dat,dist="Weibull")

## [1] "Adjustments to 95 % simultaneous confidence bounds to account for"
## [1] "non-increasing values follow method of Meeker & Escobar (1998)"

title("Figure 7", adj=1)

3. Fit models and estimate parameters.

First, we fit the Weibull model using the Lifedata.MLE() function of the SPREDA package.

exa1.spreda <- Lifedata.MLE(Surv(time,event)~1,
                            data=exa1.dat,
                            dist="weibull")
summary(exa1.spreda)

## Call:
## model.frame(formula = Surv(time, event) ~ 1, data = exa1.dat)
## 
## Parameters:
##                  mean        std 95% Lower 95% Upper
## (Intercept) 3.0595060 0.08450988 2.8938666  3.225145
## sigma       0.8906071 0.05894954 0.7822469  1.013978
## 
## Loglikelihod:
## [1] -492.5143
## 
## Covariance matrix:
##              [,1]         [,2]
## [1,]  0.007141919 -0.001552141
## [2,] -0.001552141  0.003475048
## 
## Survival probability:
##   [1] 0.048934440 0.750964862 0.374068348 0.750964862 0.015487368
##   [6] 0.354855552 0.069736281 0.271471160 0.716968860 0.437344331
##  [11] 0.174647555 0.354855552 0.858315281 0.147520242 0.001400637
##  [16] 0.821776662 0.336530164 0.374068348 0.030296987 0.415281940
##  [21] 0.374068348 0.684020172 0.895288306 0.012869483 0.785937240
##  [26] 0.484526659 0.257111426 0.509700112 0.750964862 0.821776662
##  [31] 0.821776662 0.895288306 0.058451987 0.652163102 0.184684971
##  [36] 0.652163102 0.750964862 0.509700112 0.257111426 0.895288306
##  [41] 0.621422754 0.354855552 0.460416631 0.271471160 0.271471160
##  [46] 0.460416631 0.621422754 0.821776662 0.785937240 0.858315281
##  [51] 0.621422754 0.858315281 0.750964862 0.785937240 0.858315281
##  [56] 0.895288306 0.621422754 0.591810018 0.652163102 0.394200094
##  [61] 0.591810018 0.652163102 0.785937240 0.437344331 0.104744406
##  [66] 0.286562177 0.716968860 0.048934440 0.484526659 0.785937240
##  [71] 0.621422754 0.563325060 0.821776662 0.652163102 0.104744406
##  [76] 0.750964862 0.785937240 0.821776662 0.684020172 0.750964862
##  [81] 0.062002910 0.165123214 0.243453079 0.008863639 0.484526659
##  [86] 0.621422754 0.563325060 0.374068348 0.750964862 0.858315281
##  [91] 0.374068348 0.415281940 0.821776662 0.022368118 0.019796664
##  [96] 0.750964862 0.394200094 0.535959861 0.184684971 0.484526659
## [101] 0.785937240 0.437344331 0.821776662 0.055097026 0.895288306
## [106] 0.684020172 0.821776662 0.716968860 0.484526659 0.858315281
## [111] 0.394200094 0.621422754 0.750964862 0.858315281 0.591810018
## [116] 0.147520242 0.621422754 0.509700112 0.124401513 0.230466881
## [121] 0.895288306 0.243453079 0.271471160 0.858315281 0.684020172
## [126] 0.716968860 0.785937240

This function uses, as its first argument, a formula for the model. This is formulated using the Surv() function from the dependent survival package. Type help(Surv) for further information on this function, which can handle different types of reliability data, including interval data. The terms to the right of the ~ are the explanatory terms in the model - here we type a 1 to denote that there are no additional explanatory terms.

The estimated parameters by this model are transformed parameters \(\mu\) (Intercept) and \(\sigma\) (sigma), following Meeker and Escobar (1998). To obtain the MLEs of the Weibull parameters, we need to back-transform these estimates, each for \(\hat{\beta}\)

(beta.spreda <- 1 / unname(exp(exa1.spreda$coef[2])))

## [1] 1.12283

(The unname() function is required to remove the label assigned to each of the respective coefficients, which are elements of the returned exa1.spreda object.)

and for \(\hat{\eta}\)

(eta.spreda <- unname(exp(exa1.spreda$coef[1])))

## [1] 21.31702

We can also obtain approximate 95 % confidence limits for \(\hat{\beta}\) and \(\hat{\eta}\) using these functions and the confidence limits obtained for the \(\hat{\sigma}\) and \(\hat{\mu}\) MLEs:

beta.95cl_hi <- 1 / (summary(exa1.spreda)$coefmat["sigma","95% Lower"])
beta.95cl_lo <- 1 / (summary(exa1.spreda)$coefmat["sigma","95% Upper"])
eta.95cl_lo <- exp(summary(exa1.spreda)$coefmat["(Intercept)","95% Lower"])
eta.95cl_hi <- exp(summary(exa1.spreda)$coefmat["(Intercept)","95% Upper"])
(beta.ests <- c(lower=beta.95cl_lo,est=beta.spreda,upper=beta.95cl_hi))

##     lower       est     upper 
## 0.9862148 1.1228296 1.2783688

(eta.ests <- c(lower=eta.95cl_lo,est=eta.spreda,upper=eta.95cl_hi))

##    lower      est    upper 
## 18.06302 21.31702 25.15723

As explained in Meeker and Escobar (1998), this is appropriate for those quantities that are a monotonic function of another parameter. For quantities that depend on more than one parameter more sophisticated methods may be required to obtain accurate interval estimates. As shown for the last two lines of code, enclosing a whole line within brackets will print the result (i.e., eta.ests) to the console. This is an efficient way to assign a name to an R object, as well as inspecting its value(s).

So, how well does this model fit our data? To visually assess this, we can superimpose on the Weibull probability plot the fitted model (linear on this scale) and see whether it falls within the simultaneous 95% confidence bands for the \(\hat{F}(t)\):

Probability.Plots(exa1.dat,dist="Weibull")

## [1] "Adjustments to 95 % simultaneous confidence bounds to account for"
## [1] "non-increasing values follow method of Meeker & Escobar (1998)"

# Get transformed time (x axis) and Fhat (y axis) values: 
Weibull.xval <- log(Calculate.Fhat(exa1.dat)$time)
exa1.Fhat    <- Calculate.Fhat(exa1.dat)$Fhat
Weibull.yval <- log(-log(1-exa1.Fhat))
# Get intercept and slope of mle fit on linear scale:
Weibull.slope     <- 1 / beta.spreda
Weibull.intercept <- log(eta.spreda)
# Plot as a red coloured line:
lines(x = Weibull.slope*Weibull.yval + Weibull.intercept,
      y = Weibull.yval,
      col='red', lwd=2)
title("Figure 8", adj=1)

According to this criterion, the fit of the Weibull model is consistent with these data as it falls within the 95% simultaneous confidence bounds. However, there may be other models that may fit the data equivalently well or better (e.g., Lognormal?). But you get the idea.

The joint uncertainty of the estimated Weibull model parameters is presented as the 95 % confidence region calculated for \(\hat{\beta}\) and \(\hat{\eta}\). A plot is generated using Weibull.Confidence.Region():

Weibull.Confidence.Region(data=exa1.dat,
                          model=exa1.spreda,
                          probability=0.95,
                          show.contour.labels="FALSE",
                          title="Figure 9")

The probability argument is used to specify the probability level (i.e., \(1-\alpha\)) and thus is a value between 0 and 1. An additional steps argument can be set if desired, whereby increasing its value above the default of steps=100 increases the number of values to step through for each parameter, thus increasing the resolution (and time taken) for calculating the plotted values. The time taken increases exponentially with number of steps, so we suggest not increasing this value by too much.

If you want to show confidence regions for different probability levels on the same plot, for instance, enter probability=c(0.05,0.5,0.9,0.95) for the probability argument, as well as show.contour.labels="TRUE".

4. Inference.

What can we learn about the reliability of this component or system from this fitted model?

Well, firstly, the value of \(\hat{\beta}=\) 1.12 is near 1, and the approximate 95% confidence interval for \(\hat{\beta}\) of [0.99, 1.28] contains 1, which suggests that there is neither evidence for failures predominantly occurring due to ageing or wearout effects (i.e., \(\hat{\beta}\) is not high), nor due to early failures, such as may occur due to manufacturing defects (i.e., \(\hat{\beta}\) is not low).

• Plot the failure rate or hazard function \(h(t)\), which describes the likelihood of failure during the next time increment \(\left(\mathrm{i.e.,}\qquad dR/dt=-h(t)R(t)\right)\), using:

hazard.plot.w2p(beta=beta.spreda,eta=eta.spreda,time=exa1.dat$time,line.colour="blue")
title("Figure 10", adj=1)

As the \(\hat{\beta}\) is only slightly above 1 and below 2, we knew that there was not a large increase in the failure rate with increasing time. A steeper increase in the hazard function occurs earlier, than later, in the life of this component or system (given model assumptions).

• Plot the Reliability function \(R(t)\).

Reliability.plot.w2p(beta=beta.spreda,eta=eta.spreda,time=exa1.dat$time,line.colour="blue")
# Then add a vertical line at t=30 to this plot:
abline(v=30,col="lightgray",lty=2)
title("Figure 11", adj=1)

This shows the trend of Reliability (the probability that the component or system is still functioning at time \(t\)) with \(t\).

• Calculate probability of failure (Unreliability) by time 30\(t\)

Calc.Unreliability.w2p(beta=beta.spreda,eta=eta.spreda,time=30)

## [1] 0.7695331

So, in terms of the above plot, the corresponding Reliabilty by time 30\(t\) is:

(Rel.30 <- round(1 - Calc.Unreliability.w2p(beta=beta.spreda,eta=eta.spreda,time=30),3))

## [1] 0.23

Check this by calculating the corresponding time to get this Reliability (input argument R) using Calc.Warranty.w2p():

Calc.Warranty.w2p(beta=beta.spreda,eta=eta.spreda,R=Rel.30)

## [1] 30.03691

Checks out, aside from a small rounding error.

• MTTF

Calculate the MTTF from the \(\mathbb{E}[T]\) using \(\hat{\beta}\) and \(\hat{\eta}\).

(MTTF.exa1 <- Weibull.2p.Expectation(eta=eta.spreda,beta=beta.spreda))

## [1] 20.43413

Now, in order to calculate the 95% Confidence intervals for MTTF we can obtain relatively accurate estimates using a computer-intensive method known as bootstrapping. Here we use the “bias-corrected percentile” method (e.g., see Section 13.7 of Meeker and Escobar (1998)), although there are other methods (e.g., studentized or “bootstrap-t” method). On a standard laptop this may take 10-15 mins to run, so you may want to get a cup of tea before running …

set.seed(123) # for reproducibility.
(aa <- Sys.time())

## [1] "2016-06-30 10:31:51 PDT"

MTTF.boot.95CI.bca <- boot(data=exa1.dat,
                           statistic=MTTF.boot.percentile.adj,
                           R=10000)
MTTF.boot.95CI.bca

## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = exa1.dat, statistic = MTTF.boot.percentile.adj, R = 10000)
## 
## 
## Bootstrap Statistics :
##     original       bias    std. error
## t1* 20.43413 -0.005520229    1.848863

(MTTF.boots.bca <- boot.ci(MTTF.boot.95CI.bca,conf=0.95,type="bca"))

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 10000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = MTTF.boot.95CI.bca, conf = 0.95, type = "bca")
## 
## Intervals : 
## Level       BCa          
## 95%   (17.26, 24.66 )  
## Calculations and Intervals on Original Scale

bb <- Sys.time()
(Time.taken <- bb-aa)

## Time difference of 11.49119 mins

MTTF.95cl_lo <- MTTF.boots.bca$bca[length(MTTF.boots.bca$bca)-1]
MTTF.95cl_hi <- MTTF.boots.bca$bca[length(MTTF.boots.bca$bca)]
(MTTF.ests <- c(lower=MTTF.95cl_lo,est=MTTF.exa1,upper=MTTF.95cl_hi))

##    lower      est    upper 
## 17.25680 20.43413 24.65681

Compare the MTTF to an empirical estimate for the non-censored failures:

mean(exa1.dat[exa1.dat$event==1,"time"])

## [1] 19.34959

That this value is close to the Weibull MLE for \(\mathbb{E}[T]\) likely reflects that there was a relatively small proportion of censored measurements in this dataset. See Ebeling (1997), pp 286—302, for further information on empirical estimation.

Plot the estimated Weibull pdf of t, with \(\mathbb{E}[T]\) superimposed as a vertical solid line, with the approximate 95% confidence bounds for \(\mathbb{E}[T]\) shown as dashed lines.

xfit <- seq(0,max(exa1.dat$time),by=0.01)

mle.pdf <- dweibull(xfit,shape=beta.spreda,
                     scale=eta.spreda)
plot(xfit,mle.pdf,type='l',col='red',
     xlab="Time To Failure",ylab="f(t)",
     ylim=c(0,1.25*max(mle.pdf)),bty='l',
     las=1,adj=0.5,cex.lab=1.2,cex.axis=0.85)

lines(rep(MTTF.exa1,2),c(0,dweibull(MTTF.exa1,
      shape=beta.spreda,scale=eta.spreda)),
      lwd=2,col='red')
lines(rep(MTTF.95cl_lo,2),c(0,dweibull(MTTF.95cl_lo,
      shape=beta.spreda,scale=eta.spreda)),lty=2,
      lwd=2,col='red')
lines(rep(MTTF.95cl_hi,2),c(0,dweibull(MTTF.95cl_hi,
      shape=beta.spreda,scale=eta.spreda)),lty=2,
      lwd=2,col='red')
title("Figure 12", adj=1)

Compare this to Figure 5, a histogram of the non-censored time measurements. As it looks similar, and given the relatively small proportion of censored measurements in this dataset, this is further evidence to infer that this model has adequately captured the properties of this dataset. However, more formal tests could be conducted (see Meeker and Escobar, 1998). This also demonstrates that the Weibull distribution is quite flexible in that it can approximate the Exponential distribution (when \(\beta=1\)) as well as right-skewed and symmetric unimodal distributions. We can also see that the approximate 95 % confidence interval for \(\mathbb{E}[T]\), our estimate of mean time to failure, is non-symmetrical, reflecting the skewed distribution of failure times.

Importantly, parameter estimates should be interpretted in context of knowledge of the system and of the sampled data. That is, do these results make sense? What does this mean for maintenance of this system?